ワイ、円周率を割り切った模様 → 円周率=7825万6779 分の 2億4585万922

こんにちは。 3.14から始まる円周率はどこまでも続く男のロマン・・・そんな風に考えていた時期が、ワイにもありました。 「円周率が10桁で割り切れた」とかいう嘘記事が虚構新聞から出回ったりしたこともありました。 しかしさっきプログラムを作っていろいろ計算していたところ、円周率が割り切れてしまったので報告させてください。 そもそもは、円周率を分数で表現する手法を最近知り興味を持ったのがきっかけです。例えば
とかです。7分の22が円周率のそこそこの近似値(3桁まで正しい)になっています。 次に有名なのが、
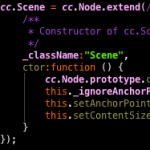
らしいです。この113分の355はなんと7桁まで正しい近似になってます。3桁の整数2つ覚えるだけで、円周率7桁分の精度が得られるとは何ともお得な数です。 ここで疑問が湧きました。 この調子で分母の整数値を上げていったらどうなるのだろうか・・・? 本来数学でのやりかただと、ここで「連分数」などを持ち出すようなのですが、幸い?自分はそのあたりは忘れてしまったソフト屋なので、力技で結論だけだす以下のようなプログラムを作りました。言語は JavaScript で、実行には Node.js を使いました。
<pi.js>
分母を1から1ずつ上げていき、分子は既知の円周率 Math.PI から逆算してます(ちょっとずるいですが・・)。 実行結果は以下の通りです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
<strong><span style="color: #808080;"> $</span> node pi.js</strong> 3/1 = 3, ERR=0.14159265358979312 13/4 = 3.25, ERR=0.10840734641020688 16/5 = 3.2, ERR=0.05840734641020706 19/6 = 3.1666666666666665, ERR=0.025074013076873403 <strong> 22/7 = 3.142857142857143, ERR=0.0012644892673496777</strong> 179/57 = 3.1403508771929824, ERR=0.0012417763968106676 201/64 = 3.140625, ERR=0.000967653589793116 223/71 = 3.140845070422535, ERR=0.0007475831672580924 245/78 = 3.141025641025641, ERR=0.0005670125641521473 267/85 = 3.1411764705882352, ERR=0.00041618300155787935 289/92 = 3.141304347826087, ERR=0.0002883057637061981 311/99 = 3.1414141414141414, ERR=0.00017851217565167943 333/106 = 3.141509433962264, ERR=0.0000832196275291075 <strong> 355/113 = 3.1415929203539825, ERR=2.667641894049666e-7</strong> 52163/16604 = 3.141592387376536, ERR=2.662132572162079e-7 52518/16717 = 3.1415923909792425, ERR=2.6261055063869776e-7 52873/16830 = 3.141592394533571, ERR=2.5905622225153024e-7 53228/16943 = 3.1415923980404887, ERR=2.555493043843171e-7 53583/17056 = 3.141592401500938, ERR=2.5208885512384427e-7 53938/17169 = 3.1415924049158366, ERR=2.4867395653771496e-7 <span style="color: #808080;"> : (中略) :</span> 5419351/1725033 = 3.1415926535898153, ERR=2.220446049250313e-14 42208400/13435351 = 3.1415926535897722, ERR=2.0872192862952943e-14 47627751/15160384 = 3.141592653589777, ERR=1.5987211554602254e-14 53047102/16885417 = 3.141592653589781, ERR=1.199040866595169e-14 58466453/18610450 = 3.1415926535897842, ERR=8.881784197001252e-15 63885804/20335483 = 3.141592653589787, ERR=6.217248937900877e-15 69305155/22060516 = 3.141592653589789, ERR=3.9968028886505635e-15 74724506/23785549 = 3.141592653589791, ERR=2.220446049250313e-15 80143857/25510582 = 3.1415926535897927, ERR=4.440892098500626e-16 <span style="color: #ff0000;"><strong> 245850922/78256779 = 3.141592653589793, ERR=0</strong></span> DONE with i=78256779 <span style="color: #808080;"><strong>$ </strong></span> |
なんと、分母が7825万6779になったところで誤差が0になって割り切れてしまいました。やばい。 つまり
であることが確かめられてしまいました。 少なくとも JavaScript さんは 円周率 = 7825万6779 分の 2億4585万922 だと判定しました。 どこか計算間違っているんでしょうかね・・・?
だれか詳しい人教えてください。
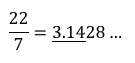
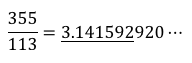
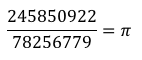



外部から失礼、
たぶん、コンピュータの量子化の問題だと思います。
分数や無理数は量子化で認識出来る’目盛り’の大きさで丸め込まれます。
例えば、28.16…mmの線分を定規で測るとき、その定規の最小目盛りが1mmだとすれば、28mmと読み上げるようにコンピュータにも最小目盛りを持ち、今回の場合は目盛りサイズが1*10^-16くらいとなります。
つまり、円周率も分数も小数点以下18桁以下は全て0として扱われるため誤差が0になるわけである。
ちなみに、wolfram言語で計算するとたぶん答えが出ないと思います。
Math.Piで与えられるπが近似値で、その近似値との誤差がなくなったということですよね。
桁数を十分にあげれば、あり得る話です。
単純に浮動小数の分解能を超えただけです
(指摘の通りMath.Pi≠πであり近似値)
無理数(分数では表せない数)というのは数学的に証明できます
https://ja.wikipedia.org/wiki/%E5%86%86%E5%91%A8%E7%8E%87%E3%81%AE%E7%84%A1%E7%90%86%E6%80%A7%E3%81%AE%E8%A8%BC%E6%98%8E
浮動小数について
https://ja.wikipedia.org/wiki/%E6%B5%AE%E5%8B%95%E5%B0%8F%E6%95%B0%E7%82%B9%E6%95%B0
これらをまず理解してからの方がいいと思います
また、2進数においては任意の桁を計算できるのでこちらも参考の事
BBP系公式
http://xn--w6q13e505b.jp/formula/bbp.html
node.jsが使っているMath.PIの実装を見てきましたが、単に数値として”3.1415926535897932″を返すだけのようですね。
それなら分数と一致するのも納得です。
なんj民が無知晒してて草
Excelで連分数使って80143857/25510582まで求めた。
数字で検索したらたどり着きましたw